Cal Poly - San Luis Obispo
Senior Theses
2005
Anne Louise Humphrey
"Expected Value of Sample Information"
Advisor: Allan Rossman (arossman@calpoly.edu)
The purpose of this project is to explore and make observation on expected value
of sample information (EVSI). In general, this is a large topic so I looked
at a particular example where I had two weighted coins, coin X and coin Y, where
the probability of getting heads with coin X is 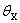 and the probability of getting heads with coin Y is
and the probability of getting heads with coin Y is 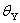 .
I started off looking at cases where
.
I started off looking at cases where 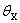 and
and 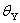 have a discrete prior
probability distribution and then moved on to cases where
have a discrete prior
probability distribution and then moved on to cases where 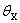 and
and 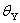 have a continuous prior
probability distribution, namely the beta distribution, which was used because
it is the conjugate prior for the binomial distribution.
have a continuous prior
probability distribution, namely the beta distribution, which was used because
it is the conjugate prior for the binomial distribution.
Amanda King
"Survey of Statistical Background and Habits of California Secondary
Mathematics Teachers"
Advisor: Beth Chance and Allan Rossman (bchance@calpoly.edu, arossman@calpoly.edu)
Statistics at the high school level is a relatively new development
and little is known about the learning and teaching environment of
Statistics at the high school level. The purpose of this research
study was to gain information about the high schools that offer Statistics,
the methods being used to teach Statistics and the preparation of teachers
teaching Statistics at the high school level.
Nick Magill
"Is
There a Better Way to Play the World Series?"
Advisor: Allan Rossman (arossman@calpoly.edu)
The goal of this project was to determine if there is a better set up for the World Series
other than a best-of seven. The analysis was based on the typical best-of series as well
as a new one. The second series analyzed was one in which a team wins as soon as it is
ahead by two games. In order to determine which series was better, two measures were
taken and a third was created. The best series was determined to be one which has a high
probability of choosing the better team as the winner and doing so in a minimum number of
games. A loss function was then created to measure the utility of each type of series.
In doing this analysis some interesting results were found. I found that if there is
a large gain associated with choosing the better team as the winner then for the most
part, the classic best of series is the best. When there is less gain associated with
choosing the better team as the winner, then the new win by two series can be found to
have the most utility.
Aaron
Quan
"Parity and Competitive Balance in Professional Sports"
Advisor: Allan Rossman (arossman@calpoly.edu)
Many have suggested that there is more parity or competitive balance in the
National Football League (NFL) recently. In this report I analyzed the trends
in parity over time, starting in 1966, in three professional sports: NFL, MLB,
and NBA. I define various measures of parity and then analyze how the parity
measures have changed over the past forty years in each sport. I also simulated
NFL seasons under a model of perfect parity to determine the distribution of
certain measures of parity. I also considered how much a team's record fluctuates
from one season to the next as another measure of parity. Finally, I compare
a sport's parity measures before and after the advent of free agency in each
sport to see if there is a significant difference in the level of competitive
balance.
2003
Colleen Kreutner
"Investigating Extensions of the Secretary Problem"
Advisor: Allan Rossman (arossman@calpoly.edu)
This project is an investigation into the famous "Secretary Problem." The Secretary Problem is a problem in which a person is trying to select the optimal object, for example the best secretary among a group of applicants. A number of people have studied this problem rather in depth. The original problem's solution can be derived using calculus and probability. The extension of the problem that I analyze is studied through enumeration and simulation.
The original Secretary Problem investigates the best strategy to select the best secretary. This problem is interesting but restricted in that any selection other than the very best applicant is considered a failure. Instead of only being interested in the best candidate, I will consider other criteria such as selecting a candidate in the top three. Also, in looking at these other cases I will also discuss the best strategy in obtaining the candidate. The strategy changes according to the number of total candidates chosen from and depending on the range the candidate is to be chosen with in.
In this extension of the Secretary Problem, I will also discuss the average rank of the candidate selected. The optimal average rank would be when the average rank is minimized, meaning that the candidate selected ends up as close as possible to the top, or the best. The average rank is also dependent on the total number of candidates being considered. I will also explore the strategy in obtaining the smallest average rank of the selected candidate.
David Schumann
"Baseball's Pythagorean Theorem"
Advisor: Allan Rossman (arossman@calpoly.edu)
Bill James created a formula that related the number of runs a baseball team
scored and allowed to its winning percentage. The formula took on the form 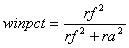 ,
where rf is the number of runs that were scored by the team and ra is the number
of runs that were scored against the team during the regular season. The general
form of the equation as shown above used a power of two to keep the model simple
and understandable. This exponent was not however the one that minimized the
error when predicting a teams winning percentage. I analyzed major league baseball
data from 1996 to 2002, calculating the root mean square error (RMSE) for the
typical exponent of 2 and others in an attempt to find the optimum exponent
value. I also used a regression approach to estimate the optimal value of the
exponent. Then I applied this Pythagorean analysis to winning percentages in
professional football, basketball, and hockey.
,
where rf is the number of runs that were scored by the team and ra is the number
of runs that were scored against the team during the regular season. The general
form of the equation as shown above used a power of two to keep the model simple
and understandable. This exponent was not however the one that minimized the
error when predicting a teams winning percentage. I analyzed major league baseball
data from 1996 to 2002, calculating the root mean square error (RMSE) for the
typical exponent of 2 and others in an attempt to find the optimum exponent
value. I also used a regression approach to estimate the optimal value of the
exponent. Then I applied this Pythagorean analysis to winning percentages in
professional football, basketball, and hockey.